電験三種の電気数学-18

amazon　kindle版の「電験三種の電気数学」に関する本を出版しました。

そちらも見て下さい。

数字の基礎、集合と論理式です。

---

1　集合

　集合は昭和の時代には小学校で勉強していました。つまり、論理的な思考をしていれば、比較的簡単な内容であるということです。

　集合はある一定の法則を持つ集まりであると言えます。例えば、「A：5以下の自然数」という集合は次のようになります。

A={1,2,3,4,5}

ここで、1,2,3,4,5は集合Aの要素と呼ばれ、1∈A、2∈A・・・と記述します。

また、集合「B：3以下の自然数」と言う集合にすると、次のようになります。

B={1,2.3}

　このとき、Bの全ての要素はAの要素に含まれるので、A⊃Bとなります。

AとBの要素が等しいときA=Bとなります。

全ての要素を全体集合Uと呼びます。

全体集合U={x｜xは10未満の自然数}として、

A={1,2,3,4,5}、B={1,3,5,7,9}という集合があります。

共通部分A∩B＝｛1,3,5｝和集合A∪B={1,2,3,4,5,7,9}
Aに含まれない数は補集合$\overline{A}$={6,7,8,9}

図のような関係になります。この図をフェン図またはベン図と呼びます。

要素が全くない集合を、空集合$\varnothing $と呼びます。

次のような関係式をド・モルガンの法則と呼びます。

$\overline{A \cap B}＝\overline{A}  \cup  \overline{B}$

$\overline{A \cup B}＝\overline{A}  \cap  \overline{B}$

例題　U={x|xは10以下の数}、A={x|xは2の倍数}、B={x|xは3の倍数}のとき次の集合を求めなさい。

①$\overline{A}$

②$A$∪$B$

③$A$∩$B$

④$\overline{A}$∩B

⑤$A$∪$\overline{B}$

⑥$A$∩$\overline{B}$

⑦$A$∩$B$

⑧$A$∪$B$

$A$={2,4,6,8,10}$B$={3,6,9}
①$\overline{A}$={1,3,5,7,9}

②$A$∪$B$={2,3,4,6,8,9,10}

③$A$∩$B$={6}

④$\overline{A}$∩B={3,9}

⑤$A$∪$\overline{B}$＝{1,2,4,5,6,7,8,10}

$\overline{B}$＝{1,2,4,5,7,8,10}

⑥$A$∩$\overline{B}$＝{2,4,8,10}

⑦$\overline{A \cap B}$＝{1,2,3,4,5,7,8,9,10}

⑧$\overline{A \cup B}$＝{1,5,7}

2　論理記号と論理演算

　論理演算は∩(AND)、∪（OR）などの集合論的記号を代数の演算のようにあつかいます。

A∪B・・・A+B

A∩B・・・A・B

となります。表示の仕方が違うだけで、計算するときに代数的に取り扱うので、慣れ親しんだ数式となります。主な定理と公理は次のようになります。

(1)1+1=1、1・1=1

(2)0+0=0、0・0=0

(3)1+0=1、1・0=0

(4)$A$=0、$\overline{A}$=1

(5)$A+B=B+A$、$A \cdot B=B \cdot A$

(6)$A+(B+C)=(A+B)+C$、$A \cdot (B \cdot C)=(A \cdot B) \cdot C$

(7)$A \cdot A=A,A+A=A$

(8)$A \cdot (A+B)=A$

(9-1)$(\overline{A+B+C+\cdots})=\overline{A} \cdot \overline{B} \cdot \overline{C} \cdots$

(9-2)$(\overline{A \cdot B \cdot C \cdots})=\overline{A} +\overline{B} +\overline{C} +\cdots$

(9-1),(9-2)はドモルガンの定理などがあります。

3　フェン図（ベン図）とカルノー図

　集合$A$と集合$B$の関係をフェン図とカルノー図で図示した場合について示します。集合が３つまではフェン図の方が分かりやすいですが、４つ以上はカルノー図で表現しましょう。

集合が4つの場合はこのように図を書くことができます。

これとは別に真理値表を書く方法もあります。

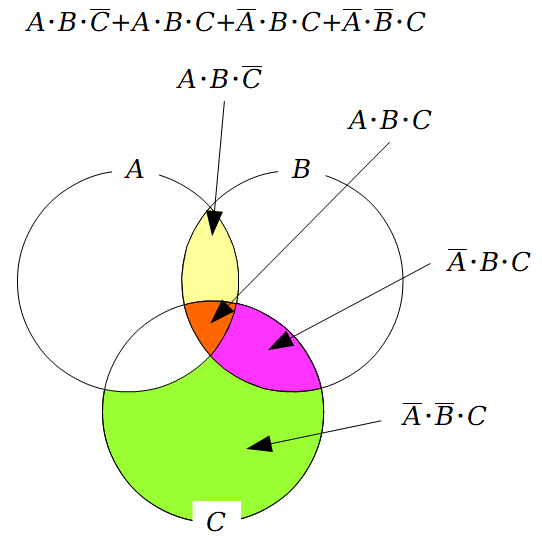
例題 $A \cdot B \cdot \overline{C}+A \cdot B \cdot C+\overline{A} \cdot B \cdot C+\overline{A} \cdot \overline{B} \cdot C$を簡単化せよ。

$X=A \cdot B \cdot \overline{C}+A \cdot B \cdot C+\overline{A} \cdot B \cdot C+\overline{A} \cdot \overline{B} \cdot C$とすると

$=A\cdot B\cdot(\overline{C}+C)+\overline{A}\cdot C（B+\overline{B}）$

$=A \cdot B+\overline{A} \cdot C$

フェン図で描くと図の着色された箇所となります。

これは$A \cdot B+\overline{A} \cdot C$と一致します。

真理値表を書くと

$A$	$B$	$C$	$A \cdot B \cdot \overline{C}$	$A \cdot B \cdot C$	$\overline{A} \cdot B \cdot C$	$\overline{A} \cdot \overline{B} \cdot C$	$X$
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 0 0 0 1 0	0 0 0 0 0 0 0 1	0 0 0 1 0 0 0 0	0 1 0 0 0 0 0 0	0 1 0 1 0 0 1 1