令和3年(2021年) 電験三種 理論 問15
amazon kindle版の「電験三種」に関する本を出版しました。
電子書籍版と紙の書籍版での購入も可能です。
そちらも、ご覧になってください。
問15は、三相回路の問題です。
これは、ベクトルを考えないといけないので、ちょっと難しいです。
解いてみましょう。
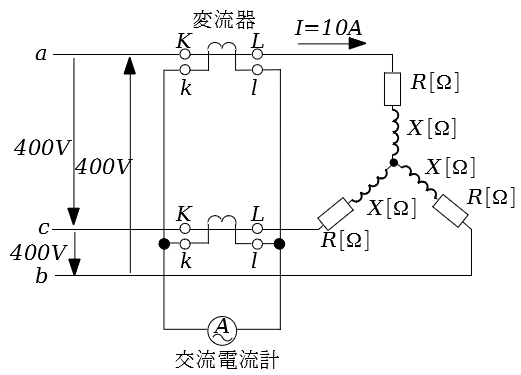
図のように，線間電圧$400V$の対称三相交流電源に抵抗$R[\Omega]$と誘導性リアクタンス$X[\Omega]$からなる平衡三相負荷が接続されている。平衡三相負荷の全消費電力は$6kW$であり，これに線電流$I=10A$ が流れている。電源と負荷との間には，変流比$20:5$の変流器が$a$相及び$c$相に挿入され，これらの二次側が交流電流計
を通して並列に接続されている。この回路について，次の（a）及び（b）の問に答えよ。
（a）交流電流計の指示値［A］として，最も近いものを次の（1）～（5）のうちから一つ選べ。
（1）$0$ （2）$2.50$ （3）$4.33$ （4）$5.00$ （5）$40.0$
（b）誘導性リアクタンス$X$の値$[\Omega]$として，最も近いものを次の（1）～（5）のうちから一つ選べ。
（1）$11.5$ （2）$20.0$ （3）$23.1$ （4）$34.6$ （5）$60.0$
解答 (a)：(2)，(b)：(1)
(a)
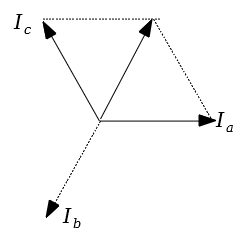
線電流$I=10A$で、変流比$20:5$の変流器より、図のベクトル$I_a$の大きさは$2.5A$となる。$I_c$の大きさも$2.5A$と等しいので、ベクトルを合成すると正三角形となるので、$2.5A$となる。
(b)
平衡三相負荷の全消費電力は$6kW$より
$P=\sqrt{3}VI \cos \theta$に代入すると
$6000=\sqrt{3} \times 400 \times 10 \times \cos \theta$
$\cos \theta=\dfrac{6000}{\sqrt{3} \times 400 \times 10}=\dfrac{3}{2 \sqrt{3}}=\dfrac{\sqrt{3}}{2}$
$\theta=30^{\circ}$
また、インピーダンスの大きさは
$|Z|=\dfrac{\dfrac{400}{\sqrt{3}}}{10}=\dfrac{40}{\sqrt{3}}$
これらから、ベクトルを描くと図のようになります。
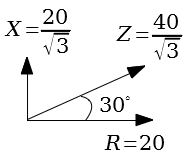
よって、
$X=\dfrac{20}{\sqrt{3}}=11.547 \fallingdotseq 11.5[\Omega]$
