令和2年(2020年) 電験三種 理論 問15
amazon kindle版の「電験三種」に関する本を出版しました。
そちらも見て下さい。
問15
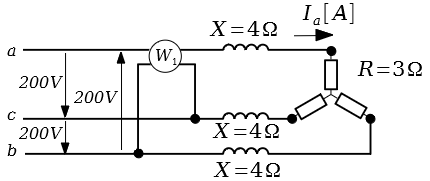
図のように,線間電圧(実効値)$ 200V $の対称三相交流電源に,1台の単相電力計$ W_1 $,$ X=4 \Omega$の誘導性リアクタンス3個,$ R=9 \Omega$の抵抗3個を接続した回路がある。単相電力計$ W_1 $の電流コイルはa相に接続し,電圧コイルはb-c相間に接続され,指示は正の値を示していた。この回路について,次の(a)及び(b)の問に答えよ。
ただし,対称三相交流電源の相順は,a,b,cとし,単相電力計$ W_1 $の損失は無視できるものとする。

(a)$ R=9 \Omega $の抵抗に流れる電流$I_{ab}$の実効値[A]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 6.77 (2) 13.3 (3)17.3 (4) 23.1 (5) 40.0
(b)単相電力計$ W_1 $の指示値[kW]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0 (2) 2.77 (3)3.70 (4) 4.80 (5) 6.40
答え (a):(2)、(b):(3)
三相回路は、そのまま計算すると分かりにくいので、1相分だけ取り出して、計算すると分かりやすくなります。ベクトルで考えないといけませんので、少し難しくなっています。
(a)負荷抵抗$9 \Omega$が$\Delta $結線されているので、これを$Y$結線にすると、抵抗は$3 \Omega$となる。
a相の線電流はインピーダンス$ Z=R+jX $より、
$Z^2=4^2+3^2=25$
$Z=5 \Omega $
相電圧は$ \dfrac{200}{\sqrt{3}} $よって、$I_a=\dfrac{200}{\sqrt{3} \times 5}=\dfrac{200}{5 \sqrt{3} }$、

また、 $I_{ab}$は、$I_a$より、位相が30°進み、大きさは$\dfrac{1}{\sqrt{3}}$なので、
$I_{ab}=\dfrac{200}{5 \sqrt{3} } \times \dfrac{1}{\sqrt{3}}=13.3 A $
(b)
単相電力計の指示は正の値を示していたので、位相は90°以内であることが分かります。
図のように、ベクトルを描くと、電力計で測定している電流は(a)で計算した、$I_a=23.09 A $となります。
ここで、$E_a $に対する、$I_a $の遅れを$\theta $で表すと
となります。$\theta=53.1^{\circ}$です。
また、$ \cos(90^{\circ}-\theta)=\sin \theta=0.8$
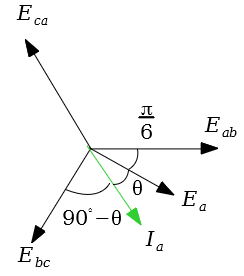
電力計はbc間に接続されているので、図に示すように$I_a $と
$E_{bc}$間の位相は$ 90^{\circ}-\theta $となります。
よって測定している電力$W_1$は$I_a$と$E_{bc}$間の位相$90^{\circ}-\theta $より
$W_1=E_{bc} I_a \cos(90^{\circ}-\theta ) $
$=200 \times 23.09 \times \sin \theta $
$=200 \times 23.09 \times 0.8 $
$=3694 W \fallingdotseq 3.7kW $