昭和50年(1975年) 電験三種 理論 問2-3 別解2

amazon　kindle版で「電験三種」に関する本を出版しました。

そちらも見ていただけるうれしいです。

---

問2はブリッジ回路をテブナンの定理を使って解く問題です。
この問題を、網目電流法を使って解いてみましょう。

　
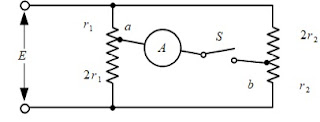
　定電圧E［V］の直流電源に$3r_1$［Ω］と$3r_2$［Ω］の抵抗を並列に接続し，かつ，図のように，各抵抗をそれぞれ1：2及び2：1に分ける点a及びbの間を電流計A及びスイッチSを通して接続してスイッチを閉じるとき，この電流計に流れる電流を求めよ。ただし，電流計の抵抗は無視するものとする。

---

解答 

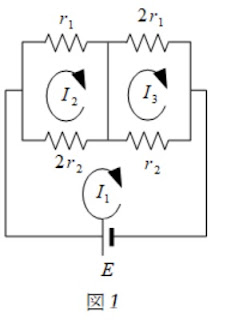
$r_1 I_2+2 r_2 (I_2-I_1)=0$・・・(1)
$2 r_1 I_3+ r_2 (I_3-I_1)=0$・・・(2)
$2 r_2(I_1- I_2)+ r_2 (I_1-I_3)=E$・・・(3)
(1)を変形して
$(r_1 +2 r_2 )I_2=2 r_2 I_1$
$I_1=\dfrac{(r_1 +2 r_2 )} {2 r_2} I_2$・・・(1)'

これを(2)式に代入すると
$2 r_1 I_3+ r_2 \left( I_3-\dfrac{(r_1 +2 r_2 )}{2 r_2} I_2 \right)=0$
$2 r_1 I_3+ r_2  I_3 -\dfrac{(r_1 +2 r_2 )}{2}  I_2 =0$
$2 (2 r_1 + r_2 ) I_3 -(r_1 +2 r_2 )  I_2 =0$
$I_2 =\dfrac{2 (2 r_1 + r_2 )} {r_1 +2 r_2 }  I_3$
$I_3 =\dfrac{r_1 +2 r_2 }{2 (2 r_1 + r_2 )}   I_2$・・・(2)'

(1)'を(3)式に代入すると
$2 r_2 \left(\dfrac{(r_1 +2 r_2 )}{2 r_2} I_2- I_2 \right)+ r_2 \left(\dfrac{(r_1 +2 r_2 )} {2 r_2} I_2-I_3 \right)=E$
$2 (r_1 +2 r_2 )  I_2-2 r_2  I_2+\dfrac{(r_1 +2 r_2 )}{2}  I_2- r_2 I_3=E$
$ 2(r_1 +2 r_2 )  I_2-4 r_2  I_2+(r_1 +2 r_2 ) I_2-2 r_2 I_3=2 E$
$(3 r_1 +2 r_2 )  I_2-2 r_2 I_3=2 E$・・・(3)'

(2)'の代入
$(3 r_1 +2 r_2 )  I_2-2 r_2 \dfrac{r_1 +2 r_2 }  {2 (2 r_1 + r_2 )}   I_2=2 E$
$(3 r_1 +2 r_2 )  I_2- r_2 \dfrac{r_1 +2 r_2 } {2 r_1 + r_2 }   I_2=2 E$
$(3 r_1 +2 r_2 )(2 r_1 + r_2)  I_2- r_2 {(r_1 +2 r_2) }   I_2=2 E(2 r_1 + r_2)$
$(6 r_1^2 +7 r_1 r_2  +2 r_2^2- r_1 r_2  -2 r_2^2)  I_2=2 E(2 r_1 + r_2)$
$(6 r_1^2 +6 r_1 r_2 )  I_2=2 E(2 r_1 + r_2)$
$I_2=2 E \dfrac{(2 r_1 + r_2)}{ (6 r_1^2 +6 r_1 r_2 )} $
$ I_2= E \dfrac{(2 r_1 + r_2) }{(3 r_1^2 +3 r_1 r_2 )} $
(2)'に代入すると

$  I_3 =\dfrac{r_1 +2 r_2 }{2 (2 r_1 + r_2 )}  \dfrac{E (2 r_1 + r_2)} { (3 r_1^2 +3 r_1 r_2 )} =E \dfrac{r_1 +2 r_2 } { (6 r_1^2 +6 r_1 r_2 )}$
$I_2-I_3= E \dfrac{(2 r_1 + r_2)}{ (3 r_1^2 +3 r_1 r_2 )} -E \dfrac{r_1 +2 r_2 }  {(6 r_1^2 +6 r_1 r_2 )}$
$= E\dfrac{(4 r_1 + 2 r_2-r_1 +2 r_2) }{(6 r_1^2 +6 r_1 r_2 )} $
$= E \dfrac{3 r_1 } {(6 r_1^2 +6 r_1 r_2 )} $
$= \dfrac{E} {2 (r_1 + r_2 )} $
となり、これで計算できました。