昭和50年(1975年) 電験三種 理論 問2-4 別解1-Maxima

amazon　kindle版で「電験三種」に関する本を出版しました。

そちらも見ていただけるうれしいです。

---

問2の問題をキルヒホッフの法則を使って解いてみました。
確認のためにmaximaで解いてみましょう。
amazon Kindle版の書籍も出版しています。書籍も参考にしましょう。

　
　定電圧E［V］の直流電源に$3r_1$［Ω］と$3r_2$［Ω］の抵抗を並列に接続し，かつ，図のように，各抵抗をそれぞれ1：2及び2：1に分ける点a及びbの間を電流計A及びスイッチSを通して接続してスイッチを閉じるとき，この電流計に流れる電流を求めよ。ただし，電流計の抵抗は無視するものとする。

---

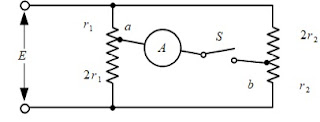
解答 

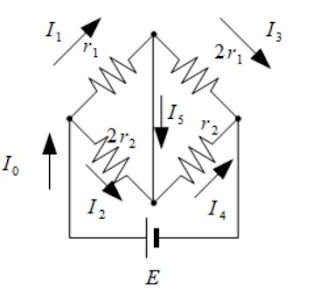
回路は図のように、ブリッジ回路にします。
電流を図の向きにおきます。
そうすると、次の式が成り立ちます。
とりあえず、成り立ちそうな式をたててみます。
$I_0=I_1+I_2$・・・(1)
$I_0=I_3+I_4$・・・(2)
$I_1=I_3+I_5$・・・(3)
$I_4=I_2+I_5$・・・(4)
$I_1 r_1-2 r_2 I_2=0$・・・(5)
$2 I_3 r_1- r_2 I_4=0$・・・(6)
$2 r_2 I_2+r_2 I_4=E$・・・(7)
$ r_1 I_1+2 r_1 I_3=E$・・・(8)

この式から(3)～(7)式までを使って、maximaで解いてみます。
linsolve([I1=I3+I5,I4=I2+I5,I1*r1-2*r2*I2=0,2*I3*r1-r2*I4=0,2*r2*I2+r2*I4=E],[I1,I2,I3,I4,I5]);
と入力します。
そうすると、
             E r2 + 2 E r1         E r2 + 2 E r1         2 E r2 + E r1         2 E r2 + E r1

(%o1) [I1 = ---------------, I2 = ---------------, I3 = ---------------, I4 = ---------------,

                          2           2                               2           2

            3 r1 r2 + 3 r1        6 r2  + 6 r1 r2       6 r1 r2 + 6 r1        3 r2  + 3 r1 r2

                                                                                               E

                                                                                     I5 = -----------]

                                                                                          2 r2 + 2 r1
これではわかりにくいので、
答えをTex表示します。
tex(%);
と入力すると、

$\left[ I_{1}={{E\,r_{2}+2\,E\,r_{1}}\over{3\,r_{1}\,r_{2}+3\,r_{1}^ 2}} , I_{2}={{E\,r_{2}+2\,E\,r_{1}}\over{6\,r_{2}^2+6\,r_{1}\,r_{2} }} , I_{3}={{2\,E\,r_{2}+E\,r_{1}}\over{6\,r_{1}\,r_{2}+6\,r_{1}^2}}  , I_{4}={{2\,E\,r_{2}+E\,r_{1}}\over{3\,r_{2}^2+3\,r_{1}\,r_{2}}}  , I_{5}={{E}\over{2\,r_{2}+2\,r_{1}}} \right] $
と出力されます。
計算結果の確認に、maxima使えますね。