amazon kindle版の「電験三種」に関する本を出版しました。
電子書籍版と紙の書籍版での購入も可能です。
そちらも、ご覧になってください。
問16は、パワーエレクトロニクスに関する問題です。
解いてみましょう。
次の文章は,単相半波ダイオード整流回路に関する記述である。
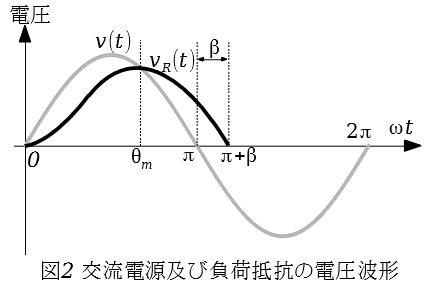
抵抗$R$とリアクトル$L$とを直列接続した負荷に電力を供給する単相半波ダイオード整流回路を図1に示す。また図1に示した回路の交流電源の電圧波形$v(t)$を破線で,抵抗$R$の電圧波形$v_R(t)$を実線で図2に示す。ただし,ダイオード$D$の電圧降下及びリアクトル$L$の抵抗は無視する。次の(a)及び(b)の問に答えよ。

ただし,必要であれば次の計算結果を利用してよい。
$\int_0^{\alpha} \sin \theta d \theta =1-\cos \alpha$
$\int_0^{\alpha} \cos \theta d \theta =\sin \alpha$
(a)以下の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
図1の電源電圧$v(t) \gt 0$の期間においてダイオード$D$は順方向バイアスとなり導通する。$v(t)$と$v_R(t)$が等しくなる電源電圧$v(t)$の位相を$\omega t=\theta_m $とすると,出力電流$i_d(t)$が増加する電源電圧の位相$\omega t$が$0 \lt \omega t \lt \theta_m $の期間においては[ (ア) ],の$\omega t=\theta_m $以降については[ (イ) ]となる。出力電流$i_d(t)$は電源電圧$v(t)$が負となっても$v(t)=0$の点よりも$\omega t=\beta$に相当する時間だけ長く流れ続ける。すなわち,$L$の磁気エネルギーが[ (ウ) ]となる$\omega t=\pi+\beta$で出力電流$i_d(t)$が$0$となる。出力電圧$v_d(t)$の平均値$V_d$は電源電圧$v(t)$を$0$~[ (エ) ]の区間で積分して一周期である$2 \pi$で除して計算でき,このとき$L$の電圧$v_L(t)$を同区間で積分すれば$0$となるので,$V_d$は抵抗$R$の電圧$v_R(t)$の平均値$V_R$に等しくなる。
| (ア) | (イ) | (ウ) | (エ) | |
|---|---|---|---|---|
| (1) | $v_L(t) \gt 0$ | $v_L(t) \lt 0$ | 0 | $\pi+\beta$ |
| (2) | $v_L(t) \lt 0$ | $v_L(t) \gt 0$ | 0 | $\pi+\beta$ |
| (3) | $v_L(t) \gt 0$ | $v_L(t) \lt 0$ | 最大 | $\pi+\beta$ |
| (4) | $v_L(t) \lt 0$ | $v_L(t) \gt 0$ | 最大 | $\beta$ |
| (5) | $v_L(t) \gt 0$ | $v_L(t) \lt 0$ | 0 | $\beta$ |
(b)小問(a)において,電源電圧の実効値$100V$,$\beta=\dfrac{\pi}{6}$のときの出力電圧$v_d(t)$の平均値$V_d[V]$として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)3 (2)20 (3)42 (4)45 (5)90
解答(a):(1),(b):(3)
(a)以下の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
図1の電源電圧$v(t) \gt 0$の期間においてダイオード$D$は順方向バイアスとなり導通する。$v(t)=v_R(t)+v_L(t)$とおける。$v(t)$と$v_R(t)$が等しくなる電源電圧$v(t)$の位相を$\omega t=\theta_m $とすると,出力電流$i_d(t)$が増加する電源電圧の位相$\omega t$が$0 \lt \omega t \lt \theta_m $の期間においては$v(t) \gt v_R(t)$なので[ (ア)$v_L(t) \gt 0$ ],の$\omega t=\theta_m $以降については$v(t) \lt v_R(t)$なので[ (イ) $v_L(t) \lt 0$ ]となる。出力電流$i_d(t)$は電源電圧$v(t)$が負となっても$v(t)=0$の点よりも$\omega t=\beta$に相当する時間だけ長く流れ続ける。すなわち,$L$の磁気エネルギーが[ (ウ)0 ]となる$\omega t=\pi+\beta$で出力電流$i_d(t)$が$0$となる。出力電圧$v_d(t)$の平均値$V_d$は電源電圧$v(t)$を$v_d(t) \gt 0$の範囲の$0$~[ (エ) $\pi+\beta$]の区間で積分して一周期である$2 \pi$で除して計算でき,このとき$L$の電圧$v_L(t)$を同区間で積分すれば$0$となるので,$V_d$は抵抗$R$の電圧$v_R(t)$の平均値$V_R$に等しくなる。
(b)
出力電圧$v_d(t)$の平均値$V_d$は電源電圧$v(t)$を$0$~$\pi+\beta$の区間で積分して一周期である$2 \pi$で除して計算できるので、
$\int_0^{\frac{7}{6}\pi} \sin \theta d \theta=1-\cos \dfrac{7}{6}\pi=1+\dfrac{\sqrt{3}}{2}=1.866$
よって、平均値$V_d$は次のように求められます。
$V_d=\dfrac{100 \sqrt{2}}{2\pi}\int_0^{\frac{7}{6}\pi} \sin \theta d \theta=\dfrac{100 \sqrt{2} \times 1.866}{2 \pi}=42.0 V$