基礎から学ぶ制御工学-20-物体の投げ上げ

基礎から学ぶ制御工学

amazon kindle版を出版しました。

---

　物体の投げ上げ

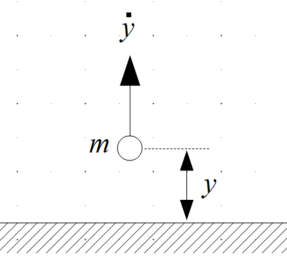
重さ$m[kg]$の物体の投げ上げを考えてみます。

上方向を$y$方向$+$とします。

運動エネルギー$T$は

$T=\dfrac{1}{2}m \dot{y}^2$

位置エネルギー$U$は

$U=mgy$

よって、ラグラジアンは

$L=T-U=\dfrac{1}{2}m \dot{y}^2-mgy$

式(3.7.2）の第1項を計算すると、

$\dfrac{d}{dt}  \left \lbrace \dfrac{\partial }{\partial \dot{y}} \left( \dfrac{1}{2}m \dot{y}^2-mgy \right) \right \rbrace$  

$=\dfrac{d}{dt}  \left(  m \dot{y} \right) $ 

$=m \ddot{y}$

式(3.7.2）の第2項を計算すると、

$\dfrac{\partial }{\partial \dot{y}} \left( \dfrac{1}{2}m \dot{y}^2-mgy \right) $

$=-mg$  

式(3.7.2）の第3項は$0$より、ラグランジュの方程式は次式となります。

$m \ddot{y}-(-mg)=0$

$m \ddot{y}=-mg$