電験三種 理論 基礎力向上テキスト-62

amazon　kindle版の本を出版しました。

そちらも見て下さい。 

---

オペアンプを用いたハイパスフィルタ-2

良く用いられるVCVS型フィルタ（二次進み系）について、見てみましょう。このフィルタも他のフィルタと同様に、図4.4.1の回路のRとCを入れ替えた回路となります。
   

    図5.4.1　オペアンプを用いたハイパスフィルタ-2

　$C_1$と$C_2$間の電圧を$V_{C1}$とし、$C_1$を流れる電流を$i_1$、$C_2$を流れる電流を$i_2$、$R_2$を流れる電流を$i_3$とすると、

$i_1=i_2+i_3$より、
$j \omega C_1(V_i-V_{R1})=j  \omega  C_2(V_{R1}-V_{+})+\dfrac{V_{R1}-V_o}{R_2}$    ・・・(5.25)

$V_{+}$には電流は流れないので、
$i_2=j  \omega C_2(V_{R1}-V_{+})=\dfrac{V_{+}}{R_1}$            ・・・(5.26)

$V_{+}=V_{-}=V_o$より、
式(5.26)を変形すると
$j \omega C_1 R_1(V_{C1}-V_o)=V_o$
$j \omega C_1 R_1V_{C1}=(1+j \omega  C_1 R_1)V_o$
$V_{C1}=\dfrac{(1+j \omega C_1 R_1)V_o}{j \omega C_1 R_1}=\left(1+\dfrac{1}{j \omega C_1 R_1} \right) V_o$    ・・・(5.27)
式(5.25)を変形すると
$j \omega C_1 R_2(V_i-V_{C1})=j \omega C_2 R_2(V_{C1}-V_o)+(V_{C1}-V_o)$

式(5.27)を代入すると

$j  \omega  C_1 R_2 \left \lbrace V_i-\left(1+\dfrac{1}{j \omega C_1 R_1} \right) V_o \right \rbrace $

$=j  \omega  C_1 R_2 \left \lbrace \left(1+\dfrac{1}{j \omega C_1 R_1} \right) V_o -V_o \right \rbrace + \left( \dfrac{1}{j \omega C_1 R_1} \right) V_o -V_o$

$j  \omega  C_1 R_2 \left \lbrace V_i-\left(1+\dfrac{1}{j \omega C_1 R_1} \right) V_o \right \rbrace =\dfrac{1+j \omega C_2 R_2}{j \omega C_1 R_1}V_o$

$ V_i-\left(1+\dfrac{1}{j \omega C_1 R_1} \right) V_o =\dfrac{1+j \omega C_2 R_2}{-( \omega C_1 R_1)^2}V_o$

$ V_i =\left(1+\dfrac{1}{j \omega C_1 R_1} \right) V_o+\dfrac{1+j \omega C_2 R_2}{-( \omega C_1 R_1)^2}V_o$

$ V_i =\dfrac{1+j \omega(C_1 R_1+ C_2 R_2)-( \omega C_1 R_1)^2}{-( \omega C_1 R_1)^2}V_o$

よって、周波数伝達関数は次式となります。
 $ \dfrac{V_o}{V_i} =\dfrac{-( \omega C_1 R_1)^2}{1+j \omega(C_1 R_1+ C_2 R_2)-( \omega C_1 R_1)^2}$       ・・・(5.28)
伝達関数の$s$に$j \omega$を代入した式が周波数伝達関数ですので、伝達関数は次式となります。
  $ G(s)=\dfrac{s^2 ( C_1 R_1)^2}{1+s(C_1 R_1+ C_2 R_2)+s^2( C_1 R_1)^2}$        ・・・(5.29)
ここで、$R_1=R_2=R$、$C_1=C_2=C$とおくと、
$ G(s)=\dfrac{s^2 ( C R)^2}{s^2( C R)^2+2 s(C R)+1}=\dfrac{s^2 ( C R)^2}{(sCR+1)^2}$    ・・・(5.30)
よって、時定数$T=CR$の2次進み系となり、折れ点周波数（カットオフ周波数）は$ \omega=\dfrac{1}{CR}$となる。

ボード線図を描いてみます。
        

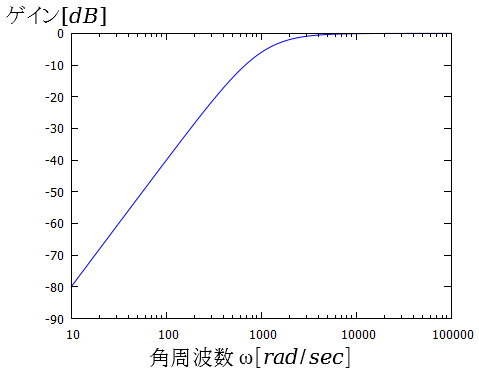
                        (a)ゲイン曲線

                          (b)位相曲線
        図5.4.2　オペアンプを用いたハイパスフィルタ