電験三種 理論 基礎力向上テキスト-59

amazon　kindle版の本を出版しました。

そちらも見て下さい。 

---

RCハイパスフィルタ
　

RCハイパスフィルタは、RCローパスフィルタのRとCが入れ替わった図5.1.1に示すような簡単な回路となっており、制御工学では典型的な一次進み形の回路となっています。

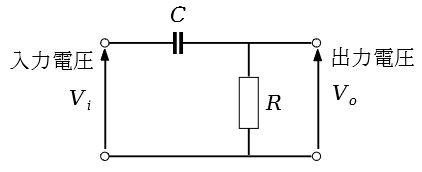
                図5.1.1　RCハイパスフィルタ

電圧の比から計算すると

$V_o=\dfrac{R}{R+\dfrac{1}{j \omega C}}V_i=\dfrac{j \omega C R}{1+j \omega C R}V_i$

よって、周波数伝達関数は次式のようになります。
$G(j \omega)=\dfrac{V_o}{V_i}=\dfrac{j \omega C R}{1+j \omega C R}$        ・・・(5.1)
微分方程式を用いて計算すると、流れる電流を$i$とすると

$V_i=\dfrac{1}{C} \int i dt +V_o$

$V_o=Ri$                            ・・・(5.2)
この式を$i$について代入すると

$V_i=\dfrac{1}{RC} \int V_o dt+V_o$

ラプラス変換すると

$V_i(s)=\left( 1+\dfrac{1}{sRC}\right) V_o$

伝達関数は次式のようになります。
$G(s)=\dfrac{V_o(s)}{V_i(s)}=\dfrac{sRC}{1+sRC}$        ・・・(5.3)
周波数伝達関数は
$G(j \omega)=\dfrac{j \omega C R}{1+j \omega C R}$             ・・・(5.4)
これは、式(5.1)と同じ式となります。

ゲインは
$\left| G(j \omega) \right|=\dfrac{ \omega C R}{\sqrt{1+ \omega^2 C^2 R^2}}$             ・・・(5.5)
位相は

$\angle G(j \omega)=\angle \dfrac{j \omega RC(1-j \omega RC)}{1+(\omega RC)^2}=\angle (\omega RC)^2+j \omega RC=\angle \omega RC+j $                    ・・・(5.6)
折れ点角周波数（カットオフ角周波数）は、時定数$T$として、
$\omega=\dfrac{1}{T}=\dfrac{1}{RC}$                ・・・(5.7)
この折れ点角周波数のとき、ゲインは
$\left| G(j \omega) \right|=\dfrac{ \dfrac{1}{RC} C R}{\sqrt{1+ \dfrac{1}{R^2 C^2} C^2 R^2}}=\dfrac{1}{\sqrt{2}}$    ・・・(5.8)
となり、ゲインの大きさは[dB]は
$20 \log \dfrac{1}{\sqrt{2}}\fallingdotseq-3dB$            ・・・(5.9)

ボード線図を描いてみます。
        

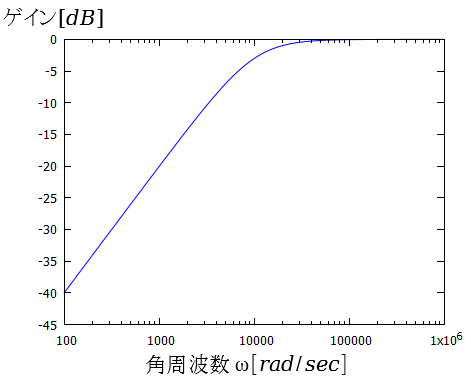
                        (a)ゲイン曲線

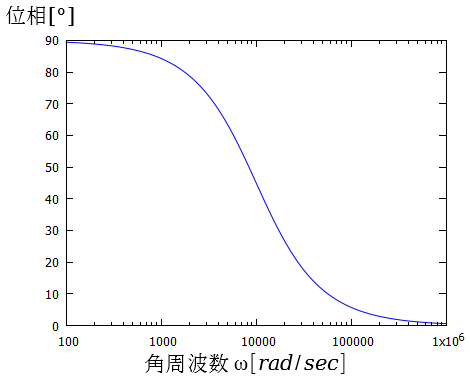
                          (b)位相曲線
        図5.1.2　RCハイパスフィルタのボード線図