電験三種 理論 基礎力向上テキスト-61

amazon　kindle版の本を出版しました。

そちらも見て下さい。 

---

オペアンプを用いたハイパスフィルタ

図5.3.1　オペアンプを用いたハイパスフィルタ（反転）

　入力インピーダンスは無限大なので、入力端子－から+へは電流は流れません。このため、$C$と$R_1$を流れる電流iは全て$R_2$に流れます。電圧降下を考えると次式のように求めることができます。
$V_i=\left( R_1+\dfrac{1}{j \omega C}\right)i+V_{-}$           ・・・(5.20)
$V_{-}=R_2 i V_o$                    ・・・(5.21)
式(5.21)を変形して

$i=\dfrac{V_{-}-V_o}{R_2}$

この式を式(5.20)に代入すると
 $V_i=\left( R_1+\dfrac{1}{j \omega C}\right)\dfrac{V_{-}-V_o}{R_2}+V_{-}$       ・・・(5.22)
$V_{+}$は接地されているので、電圧は0Vとなる。よって、式(1.1)より、$V_{-}=V_{+}=0V$を代入すると、次式のようになります。
$V_i=-\dfrac{R_1}{R_2} \left( 1+\dfrac{1}{j \omega C R_1}\right){V_o}$       ・・・(5.23)
ここで、
$R=R_1=R_2$
とすると、式(5.4)と同じ式となり、ハイパスフィルタとして動作することが分かります。

$G(j \omega)=- \left( \dfrac{j \omega C R}{1+j \omega C R}\right)$

ボード線図を描いてみます。
        

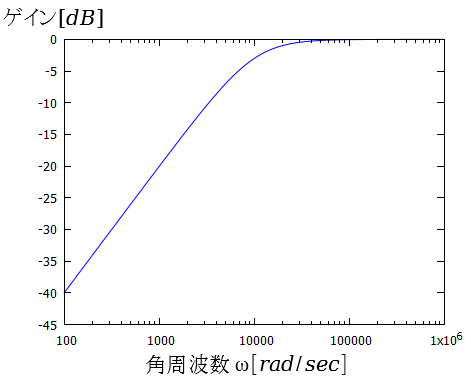
                        (a)ゲイン曲線

                          (b)位相曲線
        図5.3.2　オペアンプを用いたハイパスフィルタ