電験三種 理論 基礎力向上テキスト-50

amazon　kindle版の「最新令和2年版　電験三種（理論）基礎力向上テキスト」に関する本を出版しました。

そちらも見て下さい。 

---

テブナンの定理-3

　これまでは、変数で考えていましたが、具体的な数値で解いてみます。

解きやすいように、割ときりのいい数値にしました。

$R_1=5 \Omega, R_2=5 \Omega, R_3=15 \Omega, R_4=3 \Omega, R_5=11 \Omega, E=180 V$とします。次の、回路の$R_5$に流れる電流を求めなさい。

キルヒホッフの法則を使って解いてみましょう。

連立方程式をたてると

より、
$31 I_1- 11 I_2-15 I_3=0$
$-11 I_1+19 I_2-3 I_3=0$
$-15 I_1-3 I_2+18 I_3=180$
これならなんとか、連立方程式で解けそうですが、クラメルの公式を使って計算してみます。

$\Delta=31 \times 19 \times 18+(-11) \times (-3) \times (-15)+(-15) \times (-11) \times (-3)$
$-\{ 31 \times (-3) \times (-3)+(-11) \times (-11) \times 18+(-15) \times 19 \times (-15) \} $
$=2880$

電流を求めると、

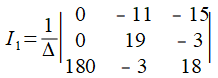
ついでに$I_3$も求めると、

よって、$R_5$を流れる電流は上から下に

流れる。