令和2年(2020年) 電験三種 理論 問10続き

amazon　kindle版の「電験三種」に関する本を出版しました。

そちらも見て下さい。 

---

  問10

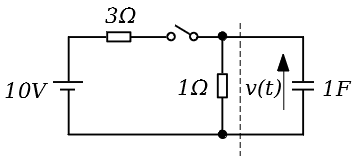
　図の回路のスイッチを閉じたあとの電圧$v(t)$の波形を考える。破線から左側にテブナンの定理を適用することで，回路の時定数［s］と$v(t)$の最終値［V］の組合せとして，最も近いものを次の（1）～（5）のうちから一つ選べ。
　ただし，初めスイッチは開いており，回路は定常状態にあったとする。

	時定数［s］	最終値［V］
（１）	0.75	10
（２）	0.75	2.5
（３）	4	2.5
（４）	1	10
（５）	1	0

---

答え　(2)

　この式を微分方程式で解くと、少し難しくなります。
図のように、電圧、抵抗、コンデンサをおきます。

このとき、微分方程式は、次の連立方程式になります。
$R_1 i_1+R_2(i_1-i_2)=E$・・・(1)
$R_2 (i_1-i_2)=\dfrac{1}{C} \int i_2 dt$・・・(2)
式(2)を変形すると
$-R_2 (i_1-i_2)+\dfrac{1}{C} \int i_2 dt=0 $・・・(2)'
(1)を変形すると

$i_1=\dfrac{E+R_2 i_2}{R_1+R_2}$

この式を(2)'に代入して変形すると

$-\dfrac{R_2 E-R_1 R_2 i_2}{R_1+R_2}+\dfrac{1}{C} \int i_2 dt=0 $

$\dfrac{R_1 R_2 }{R_1+R_2}i_2+\dfrac{1}{C} \int i_2 dt =\dfrac{R_2 E}{R_1+R_2} $
ここで、$ R_0=\dfrac{R_1 R_2 }{R_1+R_2}=0.75 \Omega  ,  E'=\dfrac{R_2 E}{R_1+R_2}=2.5V $ とし、

$ i_2=\dfrac{ d q }{ dt } $ とおけば、次式のようになります。

$ R_0 \dfrac{d q}{dt}+\dfrac{1}{C}q=E' $

この式を変数分離の方法で計算します。式を変形すると

$ \dfrac{1}{q-CE'}d q=-\dfrac{1}{CR_0} dt $

$  \log | q-CE'|=-\dfrac{1}{CR_0}t+K $

$K$は積分定数
式を変形すると

$   q-CE'=K'e^{-\dfrac{1}{CR_0}t}$
$K’$は積分定数
$ t=0 $のとき、初期状態$ q=0 $なので

$   q=CE' \left(1-e^{-\dfrac{1}{CR_0}t} \right)$

よって、時定数$T=CR_0=0.75s $、電圧の最終値は$ E'=2.5V $になります。

これらから、答えは(2)となります。