令和3年(2021年) 電験三種 理論 問1

amazon　kindle版の「電験三種」に関する本を出版しました。

電子書籍版と紙の書籍版での購入も可能です。

そちらも、ご覧になってください。

youtu.be

問1は、コンデンサの問題です。

解いてみましょう。

---

　次の文章は，平行板コンデンサに関する記述である。

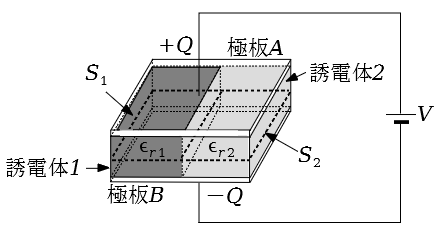
　図のように，同じ寸法の直方体で誘電率の異なる二つの誘電体（比誘電率$\epsilon_{r1}$の誘電体1と比誘電率$\epsilon_{r2}$の誘電体2）が平行板コンデンサに充填されている。極板間は一定の電圧$V$［V］に保たれ，極板Aと極板Bにはそれぞれ$+Q$［C］と$-Q$［C］（$Q \gt 0$）の電荷が蓄えられている。誘電体1と誘電体2は平面で接しており，その境界面は極板に対して垂直である。ただし，端効果は無視できるものとする。

　この平行板コンデンサにおいて，極板A，Bに平行な誘電体1，誘電体2の断面をそれぞれ面$S_1$，面$S_2$（面$S_1$と面$S_2$の断面積は等しい）とすると，面$S_1$を貫く電気力線の総数（任意の点の電気力線の密度は，その点での電界の大きさを表す）は，面$S_2$を貫く電気力線の総数の［ (ア) ］倍である。面$S_1$を貫く電束の総数は面$S_2$を貫く電束の総数の［ (イ) ］倍であり，面$S_1$と面$S_2$を貫く電束の数の総和は［ (ウ) ］である。

　上記の記述中の空白箇所（ア）～（ウ）に当てはまる組合せとして，正しいものを次の（1）～（5）のうちから一つ選べ。

	（ア）	（イ）	（ウ）
（１）	$1$	$\dfrac{\epsilon_{r1}}{\epsilon_{r2}}$	$Q$
（２）	$1$	$\dfrac{\epsilon_{r1}}{\epsilon_{r2}}$	$\dfrac{Q}{\epsilon_{r1}}+\dfrac{Q}{\epsilon_{r2}}$
（３）	$1$	$\dfrac{\epsilon_{r2}}{\epsilon_{r1}}$	$\dfrac{Q}{\epsilon_{r1}}+\dfrac{Q}{\epsilon_{r2}}$
（４）	$\dfrac{\epsilon_{r2}}{\epsilon_{r1}}$	$1$	$\dfrac{Q}{\epsilon_{r1}}+\dfrac{Q}{\epsilon_{r2}}$
（５）	$\dfrac{\epsilon_{r2}}{\epsilon_{r1}}$	$1$	$Q$

---

解答 （1）  

　電気力線の総数$n$［本］は電界の強さ（電界の大きさ）$E$［V/m］と等しくなる。
　よって、極板間の距離を$L$[m]とすると、$E=\dfrac{V}{L}$[V/m]となり、面$S_1$を貫く電気力線の総数は，面$S_2$を貫く電気力線の総数と等しくなります。

　よって、１倍となります。

次に、電束密度は$D=\epsilon E$となりますので、
誘電体1の電束は$\epsilon_0 \epsilon_{r1} E S_1$
誘電体2の電束は$\epsilon_0 \epsilon_{r2} E S_2$
面$S_1$と面$S_2$の断面積は等しいので、
面$S_1$を貫く電束の総数は面$S_2$を貫く電束の総数の

$\dfrac{\epsilon_0 \epsilon_{r1} E S_1}{\epsilon_0 \epsilon_{r2} E S_2}=\dfrac{\epsilon_{r1}}{\epsilon_{r2}}$倍となります。

最後に電束の数の総和は

$\epsilon_0 \epsilon_{r1} E S_1+\epsilon_0 \epsilon_{r2} E S_2$
$=E(\epsilon_0 \epsilon_{r1}  S_1+\epsilon_0 \epsilon_{r2}  S_2)$

$=\dfrac{V}{ L} (\epsilon_0 \epsilon_{r1}  S_1+\epsilon_0 \epsilon_{r2}  S_2)$

ここで、$C_1=\dfrac{\epsilon_0 \epsilon_{r1}  S_1}{L},C_2=\dfrac{\epsilon_0 \epsilon_{r2}  S_2}{L}$
より、

$=\dfrac{V}{ L} (LC_1+LC_2)$

$=V(C_1+C_2)$
$=VC=Q$

	（ア）	（イ）	（ウ）
（１）	$1$	$\dfrac{\epsilon_{r1}}{\epsilon_{r2}}$	$Q$